信安实验-RSA(备课)

2022-09-25 23:07:08 # 密码学 # RSA # 数论

# 简介

来源

RSA 加密算法是一种非对称加密算法。在公开密钥加密和电子商业中 RSA 被广泛使用。RSA 是 1977 年由罗纳德・李维斯特（Ron Rivest）、阿迪・萨莫尔（Adi Shamir）和伦纳德・阿德曼（Leonard Adleman）一起提出的。RSA 就是他们三人姓氏开头字母拼在一起组成的。
安全性

RSA 算法的可靠性由极大整数因数分解的难度决定。换言之，对一极大整数做因数分解愈困难，RSA 算法愈可靠。假如有人找到一种快速因数分解的算法的话，那么用 RSA 加密的信息的可靠性就肯定会极度下降。但找到这样的算法的可能性是非常小的。如今，只有短的 RSA 密钥才可能被强力方式解破。到 2017 年为止，还没有任何可靠的攻击 RSA 算法的方式。

# 前置知识

# 模运算

假设 a,r,m∈Z（Z 为整数集），并且 m>0。如果 m 除 a-r，可记作：

1	a ≡ r mod m

其中 m 为模数，r 为余数

# 余数计算

总可以找到一个 a∈Z，使得

1	a = q · m + r , 其中0 ≤ r < m

由于 a - r = q・m（m 除 a-r），上面的表达式可以写作：

1	a ≡ r mod m(r∈{0,1,2,…,m-1})

如a=88,m=12,则

88 = 12 ·7 + 4
因此88 ≡ 4 mod 12

# 等价类中所有成员得到行为等价

对于一个给定模数 m，选择等价类中任何一个元素来计算，结果都是一样的

直接计算

1	3⁸ = 6561 ≡ 2 mod 7

替代计算 (简化)

将3⁸ 替换为3⁴ ·3⁴ = 81 ·81
因为81 = 11 · 7 +4
则3⁸ = 81 · 81 ≡ 4 · 4 =16 mod 7
最后得到16 ≡ 2 mod 7

# 乘法逆元 (模逆元)

模逆元也称为模倒数。

一整数 𝑎 对同余 𝑛 之模逆元是指满足以下公式的整数 𝑏：

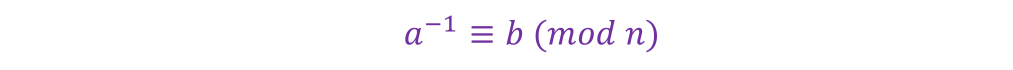
在这里插入图片描述

也可以写成以下的式子：

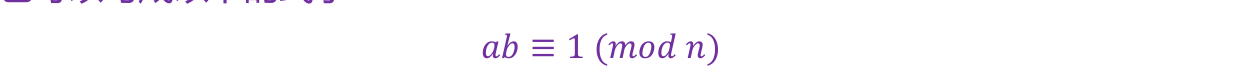
在这里插入图片描述

整数 𝑎 对模数 𝑛 之模逆元存在的充分必要条件是 𝑎 和 𝑛 互素，若此模逆元存在，在模数 𝑛 下的除法可以用和对应模逆元的乘法来达成，此概念和实数除法的概念相同。

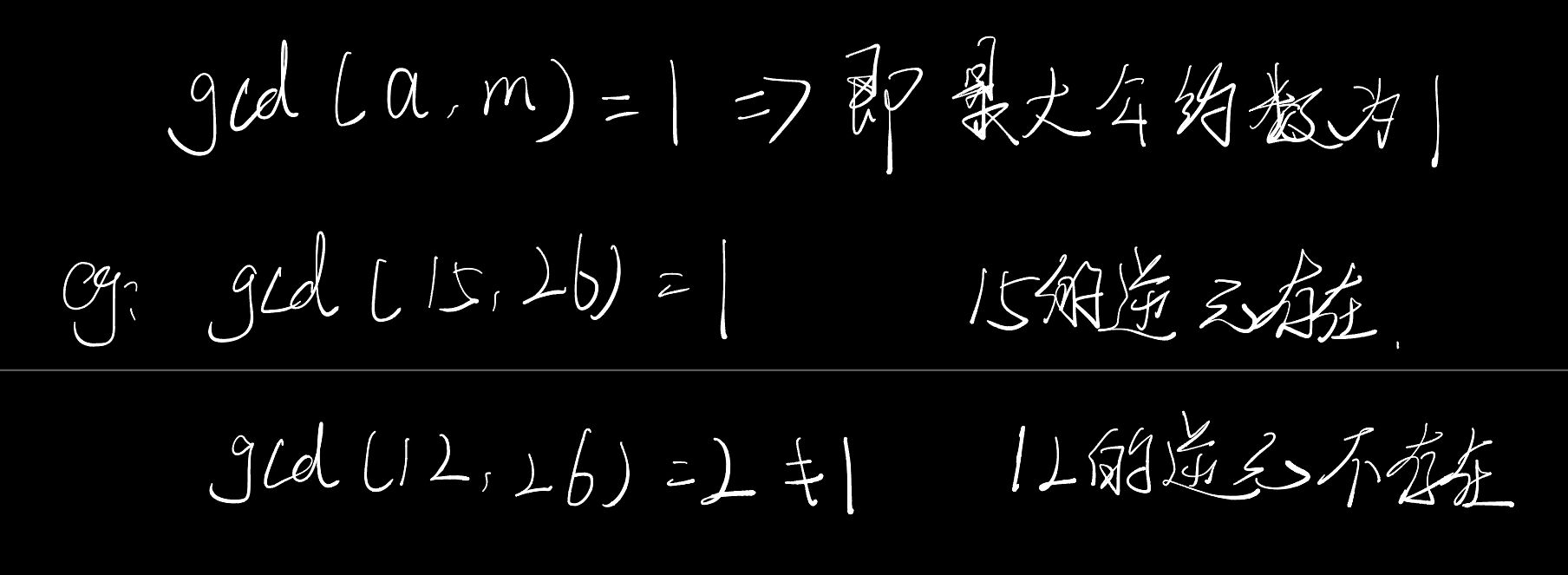
在这里插入图片描述

# Python 实现模逆元

可以使用 Python 第三方包 Crypto 的 inverse () 函数求模逆元。

from Crypto.Util.number import inverse
print(inverse(3, 7))  # 3 是要求逆元的数，7是模数

#5

可以使用 Python 第三方包 gmpy2 的 invert () 函数求模逆元。

from gmpy2 import invert
print(invert(3, 7)) # 3 是要求逆元的数，7是模数

#5

可以在 SageMath 中直接用 inverse_mod () 函数求模逆元。

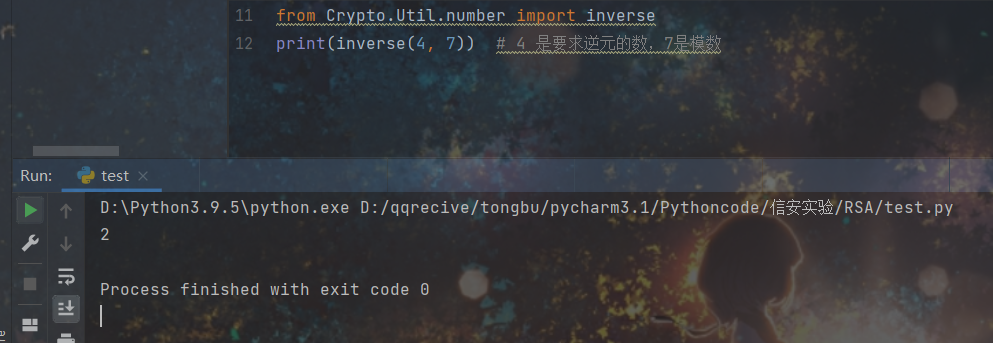
1	inverse_mod(3, 7) # 3 是要求逆元的数，7是模数

# 模运算

加法

1
2
3

3 + 4 ≡ 0 (𝑚𝑜𝑑 7)
5 + 5 ≡ 3 (𝑚𝑜𝑑 7)
1 + 5 ≡ 6 (𝑚𝑜𝑑 7)

减法

1 2	5 − 2 ≡ 3 (𝑚𝑜𝑑 7) 3 − 5 ≡ 3 − 5 + 7 ≡ 3 + 2 (𝑚𝑜𝑑 7)

乘法

1 2	3 × 4 ≡ 5 (𝑚𝑜𝑑 7) 2 × 2 ≡ 4 (𝑚𝑜𝑑 7)

模运算没有除法 (此处结合乘法逆元)

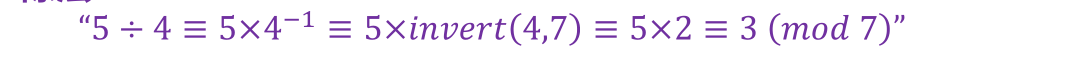
在这里插入图片描述

# 欧拉函数

Zm 内与 m 互素的整数的个数可以表示为 φ(n)

示例：

假设 m 等于 6 时，现在对应的集合为

GCD(0, 6) = 6
GCD(1, 6) = 1------互素
GCD(2, 6) = 2
GCD(3, 6) = 3
GCD(4, 6) = 2
GCD(5, 6) = 1------互素

由于该集合中，有两个与 6 互素的数字，即 1 和 5

所以欧拉函数的值为 2，即 φ(6) = 2。

φ(n)=(p-1)(q-1) //pq 为不相等的质数

# 秘钥生成

1、选择两个不相等的质数 p 和 q

2、计算 q 与 p 的乘积 n

3、计算 n 的欧拉函数 φ(n)

4、选择一个整数 e，(1<e<φ(n))，且 e 与 φ(n) 互质

5、计算 e 对于 φ(n) 的模反元素 d，公式表示为 ed≡1(modφ(n))

6、(n,e) 打包为公钥，(n,d) 打包为秘钥

# 加解密函数

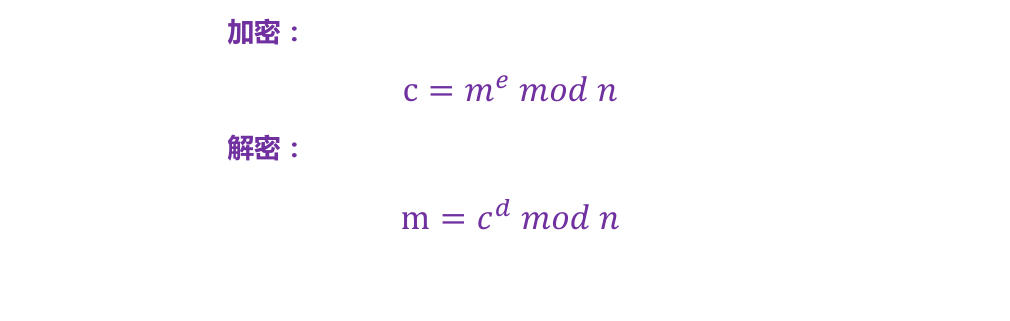
在这里插入图片描述

# 加密过程

1、首先取一个明文 m，假设为 4

2、选择不相等的质数。假设 q=3，p=11

3、计算 n=pq=33

4、计算 φ(n)=(p-1)(q-1)=(3-1)(11-1)=20

5、选择一个整数 e，假设 e=3

6、计算 d ≡ e⁻¹ ≡ 7 mod 20, 即 d = 7

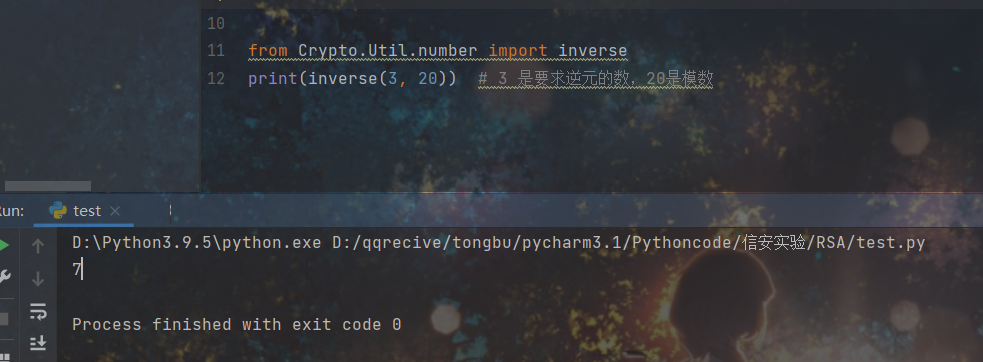
在这里插入图片描述

7、计算 mᵉ ≡ c mod n，即 64 ≡ 31 mod 33，得到 c = 33

此时得到密文 c = 31，公钥对 (33,3)，私钥对 (33,7)

# 解密过程

1、假设只知道 n=33，c=31，e=3

2、首先分解 n，n=11・3

3、计算欧拉函数 φ(n)=(11-1)・(3-1)=20

4、计算模反元素 d，根据 ed≡1(modφ(n)) ，d=(20+1)/3=7

5、解密 cᵈ ≡ m mod n ，即 31⁷ ≡ m mod 33，计算得到 m = 4

2022-09-25 23:07:08 # 密码学 # RSA # 数论